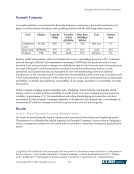
Emerging Practices for Capital Adequacy © Copyright 2003, CCRO. All rights reserved. 66 Market, credit, and operative risk can each be diversified in a portfolio: • Market – Risk reduction through fuel or geographic diversity • Credit – Risk reduction through multilateral netting, clearing, diversity of contract durations, and counterparty ratings • Operative – Risk reduction through fleet diversity (fuel, geographic location, regulatory markets) and internal controls. Diversification Benefits Available vs. Required Capital ($ millions) Coal Combined- Cycle Peaking Total Individual Assets Total Portfolio Diversified Component Risk Available Capital 50 510 11 571 571 Debt 25 255 6 286 286 Required Economical Capital Market Risk 7 28 4 39 23 -16 Credit Risk 0 0 0 0 0 0 Operative Risk 21 3 2 26 22 -4 Diversification Effect - Across Risks -10 -2 -2 -14 -11 3 Total Required Economic Capital 19 29 4 52 35 -17 Economic Capital Adequacy 6 226 1 234 251 The above table illustrates the unhedged case, where credit risk is zero. Additionally, $16 million in market risk and $4 million in operative risk are eliminated by holding the three assets as a portfolio, reflecting the benefits of diversification. Finally, the variability of the amount of capital required to run a going concern is a function of the capital required to cover all three risks – market, credit, and operative – but what function? At each level so far, the three risk components of capital adequacy (market, credit, and operative) have been calculated as part of the Monte Carlo simulation that captures the diversification effect due to these three risks being correlated. Thus, correlation coefficients, AB , can be calculated between any pair of risks A and B. Our example illustrates the mathematical fact that: EC = 0 (square root sum of squares) EC0  1 (Monte Carlo simulation) EC=1 (simple sum) The equation is true irrespective of the actual method used for computing EC as long as all other parameters (other than the pairwise correlation) are held constant. As mentioned in Section 7.3, market risk and credit loss have been studied sufficiently to determine that, while they are related, there is certainly a diversification benefit that should be captured in the combination. This benefit is lost if one uses the simple sum methodology, as illustrated by comparing the Monte Carlo results with a simple sum and square root sum of squares calculation for the unhedged portfolio.